OIA-Politecnico

Combinatoria

La combinatoria es el arte de contar.

• Gottfried Leibniz

Más concretamente, es el arte de calcular el tamaño de un conjunto sin tener que construir todos sus elementos.

Notacion: Si \( A \) es un conjunto, \( \# A \) o eventualmente \( \# (A) \) representa su tamaño.

Algunas ideas buenas:

• Principio de la suma. Si en un conjunto hay dos clases disjuntas de elementos y podemos contar el tamaño de cada clase por separado, el tamaño del conjunto es simplemente la suma de los tamaños de las dos clases.

  O sea, si \( A \) y \( B \) son conjuntos que no comparten elementos, entonces:

  \[\#(A \cup B) = \# A + \# B\]

• Principio de inclusion-exclusion. Si un conjunto está formado por dos clases que tienen elementos en común, igual se puede calcular su tamaño.

  Fijate que si sumamos los tamaños de las clases, pasa que contamos dos veces los elementos que estan en ambas clases. Entonces, podemos encontrar el tamaño real restando la cantidad de elementos comunes.

  O sea, si \( A \) y \( B \) son conjuntos, posiblemente con elementos en común, entonces:

  \[\# (A \cup B) = \# A + \# B - \# (A \cap B)\]

• Principio del producto. Si los elementos de un conjunto se pueden formar combinando libremente un elemento de un conjunto con un elemento de otro, el tamaño del conjunto es el producto de los tamaños de los dos conjuntos.

  O sea, si \( A \) y \( B \) son conjuntos, entonces:

  \[\# (A \times B) = \# A \cdot \# B\]

  Por ejemplo, ¿cuántas la cantidad de vestimentas que se pueden formar con \( 3 \) pantalones y \( 7 \) remeras? \(3 \cdot 7 = 21 \)

• Para un conjunto de tamaño \( N \), existen \( 2^{N} \) subconjuntos.

  Una forma de pensar esto es mediante el principio del producto. Para cada elemento tengo que elegir si lo agarro o no lo agarro. Esto me deja con \( N \) elecciones independientes, donde cada una tiene dos opciones.

  Entonces la cantidad es \( 2 \cdot \dots \text{ (N veces) } \dots \cdot 2 = 2^{N} \).

• Hay \( N ! = 1 \cdot 2 \cdot 3 \cdot \dots \cdot N \) formas de ordenar \( N \) objetos distintos.

  De nuevo, podemos pensarlo con el principio del producto. Para el primer elemento tenemos \( N \) opciones. Entonces quedan \( N-1 \) opciones para el segundo elemento, \( N - 2 \) para el tercero y asi sucesivamente.

• Para un conjunto de tamaño \( N \), existen \( \frac{ N ! }{ k! (N - k) ! } \) subconjuntos de tamaño \( k \).

  TODO: explicar con la idea de cocientar los que son equivalentes

• Biyecciones. Si dos conjuntos tienen igual tamaño, suele haber una buena razon para esto. En particular, debería haber una correspondencia uno a uno (o “biyección”) entre los elementos de un conjunto y los elementos del otro

  TODO: poner un ejemplo

• La misma cosa se suele poder contar de distintas formas, agrupando de formas ingeniosas.

  TODO: poner un ejemplo

• Relaciones de recurrencia. Cuando tenemos una familia de conjuntos, muchas veces podemos calcular el tamaño de un conjunto en términos de los tamaños de otros conjuntos de la familia.

  Por ejemplo, imaginate un tablero de \( 2 \times N \) casillas. ¿De cuántas formas lo podemos tapar con fichas de Dominó?

  Consideremos el conjunto de formas \( F(N) \). Si \( N=1 \) obviamente hay una sola forma. Si \( N=2 \), hay dos formas.

  

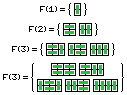
  Si \( N>2 \), entonces podemos pensar lo siguiente:

  Si ponemos una fichita vertical a la izquierda de todo, nos queda un hueco de \( 2 \times (N-1) \) y ahi podemos completar con cualquiera de las formas del conjunto \( F(N-1) \).

  Si ponemos fichitas horizontal a la izquierda de todo, nos queda un hueco de \( 2 \times (N-2) \), que podemos rellenar con cualquiera de las formas de \( F(N-2) \).

  

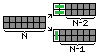
  Estos dos casos son mutuamente excluyentes. Entonces, por el principio de la suma, el tamaño del conjunto es \( \# F(N) = \# F(N-1) + \# F(N-2) \).

  Este tipo de observaciones nos permiten resolver problemas de combinatoria usando programación dinámica.

  vector<int> tam_F(N+1);
  tam_F[1] = 1;
  tam_F[2] = 2;
  for (int i = 3; i <= N; ++i) {
      tam_F[i] = tam_F[i-1] + tam_F[i-2];
  }
  

• Principio de inclusión-exclusión (cont.). Si queremos calcular el tamaño de la union de varios conjuntos, podemos generalizar la idea que usamos para dos conjuntos.

  Empezamos sumando los tamaños de todos los conjuntos.

  Pero para no contar de más, restamos los tamaños de las interseccións de cada par de conjuntos.

  El problema es que si un elemento está en tres conjuntos, lo sumamos tres veces al sumar cada conjunto y lo restamos tres veces al restar los pares de conjuntos. Para corregir esto, sumamos los tamaños de las intersecciónes de tres conjuntos.

  Pero, si un elemento está en cuatro conjuntos, lo estamos sumando de más, entonces restamos los tamaños de las intersecciones de cuatro conjuntos.

  Y así sucesivamente, sumando las intersecciones de cantidad impar de conjuntos y restando las de cantidad par.

  Hay una implementacion muy comoda usando mascaras de bits:

  int resultado = 0;
  for (int i = 0; i < (1 << N); ++i) {
      int cantidad = calcular_interseccion(i);
      if (popcount(i)%2 == 1) {
          resultado += cantidad;
      } else {
          resultado -= cantidad;
      }
  }